Sim Manager for particle GLE
Provide a class of methods for generating paths and computing physical quantities related to the motion of a spherical particle in a Generalized Roue viscoelastic fluid. The motion is described via a GLE.
Contents
The simulation method generates the covariance of the position process based on the knowledge of the covariance of the velocity process. The velocity process is Gaussian, stationary and non-Markovian. The position process is Gaussian, non-stationary and non-Markovian.
Integration is done using residue calculus.
Warning: the integral won't be correct for a high number of kernels, because finding the roots is impossible.
Warning: no method to write data to disk.
Christel Hohenegger
Last updated: 06/01/2016
classdef SimManager < handle
Output data
- Physical parameters
- Results of the residue calculus: contains the t Vector, the residues and the location of the roots omega
- Covariance matrix in block form
- Path
- Mean square displacement (MSD)
- Increment auctocorellation (ACF)
- First passage time (FPT)
- Mean first passage time (MFPT)
- Standard deviation for first passage time (SMFPT)
- Relative number of survivors
properties
parameters = [];
resCalc = [];
dataCovMatL = [];
dataPath = [];
dataMSD = [];
dataIncACF = [];
dataFPT = [];
dataMFPT = [];
dataSMFPT = [];
dataSurvivors = [];
end
methods
Method: sim initialization
Input: radius in microns, number of kernels,  Rouse exponents, number of time steps
Rouse exponents, number of time steps
function obj = SimManager(radius,numKernels,alpha,numTsteps) obj.parameters.radius = radius; obj.parameters.numKernels = numKernels; obj.parameters.alpha = alpha; obj.parameters.numTsteps = numTsteps; end
Method: delete
function delete(~) end
Method: initialize GLE's parameters
Units: [time]=milliseconds, [length]=microns, [mass]=milligrams
- Boltzman constant times temperature: length squared times mass per time squared
- Particle's density: mass per volume (close to that of water)
- Particle's mass: calculated as a sphere with the given density
- Solvent dynamic viscosity: mass per length per time (water)
- GLE parameters: a for the solvent drag, b for the polymer drag, c for the thermal fluctuations
- Relaxation times: smallest time
 , given as Generalized Rouse spectrum
, given as Generalized Rouse spectrum - G0: Mean polymer stress
- Gamma: parameter needed in the residue calculus
- Inverse relaxation times
 : parameter needed to determine the threshold of survivors
: parameter needed to determine the threshold of survivors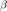 : parameter needed to increase the time steps if too many survivors
: parameter needed to increase the time steps if too many survivors
function GenerateParameters(obj) obj.parameters.kbt = 4.1e-9; obj.parameters.density = 1.05e-9; obj.parameters.mass = 4/3*pi*obj.parameters.radius.^3 ... *obj.parameters.density; obj.parameters.etasol = 1e-6; obj.parameters.aGLE = 9/2*obj.parameters.etasol... /obj.parameters.density*(1./obj.parameters.radius.^2)'; obj.parameters.cGLE = sqrt(obj.parameters.kbt./obj.parameters.mass); obj.parameters.tau0 = 1; obj.parameters.tau = obj.parameters.tau0*(obj.parameters.numKernels./... (obj.parameters.numKernels-(0:obj.parameters.numKernels-1)))... .^(obj.parameters.alpha); obj.parameters.tauavg = mean(obj.parameters.tau); obj.parameters.G0 = 1e-4; obj.parameters.bGLE = 9/2*obj.parameters.G0... /obj.parameters.density/obj.parameters.radius^2; obj.parameters.gamma = obj.parameters.bGLE/obj.parameters.numKernels; obj.parameters.lambda = 1./obj.parameters.tau; obj.parameters.dt = 1; obj.parameters.time = (0:obj.parameters.numTsteps)*obj.parameters.dt; obj.parameters.numPaths = 2e3; obj.parameters.kappa = 0.02; obj.parameters.beta = 1.1; end
Method: calculate the residues of the helper function 
Compute the poles and residues of  where
where  is written using the polynomials
is written using the polynomials 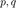 . Uses Vieta's formula. The t vector contains the coefficient of
. Uses Vieta's formula. The t vector contains the coefficient of  written as a series, the s vector contains the coefficient of
written as a series, the s vector contains the coefficient of  written as a series. Uses the recurrence formula to compute the s vector.
written as a series. Uses the recurrence formula to compute the s vector.
Computation can be done for the relaxation times labeled with New or for the inverse relaxation times commented out.
Residue is computed using the definition and the series expansion.
Commented out: check the values of the poles and residues against the knonwn value of the integral of  .
.
function ResidueCalc(obj) lambda = obj.parameters.lambda; numK = obj.parameters.numKernels; gamma = obj.parameters.gamma; aGLE = obj.parameters.aGLE; tau = obj.parameters.tau; tVec = poly(-1i*lambda); tVecNew = poly(-1i*tau); %{ sVec = zeros(1,numK+2); sVec(1,1) = tVec(1); sVec(1,2) = tVec(2)+1i*aGLE*tVec(1); for jindex=2:numK sVec(1,jindex+1) = tVec(jindex+1)+1i*aGLE*tVec(jindex)... -gamma*(numK-jindex+2)*tVec(jindex-1); end sVec(1,numK+2)=1i*aGLE*tVec(numK+1)-gamma*tVec(numK); %} sVecNew = zeros(1,numK+2); sVecNew(1,1) = 1; for jj=1:numK-1 sVecNew(1,jj+1) = (-tVecNew(jj)+aGLE*1i*tVecNew(jj+1)+... gamma*(jj+1)*tVecNew(jj+2))./(aGLE*1i*tVecNew(1)+... gamma*tVecNew(2))*(-1)^(jj); end sVecNew(1,numK+1) = (-tVecNew(numK)+aGLE*1i*tVecNew(numK+1))... ./(aGLE*1i*tVecNew(1)+gamma*tVecNew(2))*(-1)^(numK); sVecNew(1,numK+2) = prod(tau)*(-1i)^(numK)/(aGLE*1i*tVecNew(1)... +gamma*tVecNew(2)); psiVec = roots((-1).^(0:numK+1).*sVecNew); omegaVec = 1./psiVec; obj.resCalc.resVec = 1/(1i)*polyval(tVecNew,psiVec)./... (polyval((-1).^(0:numK).*sVecNew(2:end).*(1:numK+1),psiVec))... .*1./(aGLE*1i*tVecNew(1)+gamma*tVecNew(2)); %{ [~,pVec] = residue(tVec,sVec); omegaVec = conj(pVec); obj.resCalc.resVec = 1/(1i)*polyval((-1).^(0:numK).*tVec,omegaVec)./... polyval((-1).^(0:numK).*sVec(1:end-1).*(numK+1:-1:1),omegaVec); %} obj.resCalc.tVec = tVec; obj.resCalc.omegaVec = omegaVec; %{ fprintf('Roots and Residues in the positive half plane: \n') disp([omegaVec obj.resCalc.resVec]) fprintf('Check: Sum of residues %6.4f+%6.4fi = %6.4f+%6.4fi.\n',... real(sum(obj.resCalc.resVec)),imag(sum(obj.resCalc.resVec)),... real(-1i),imag(-1i)) %} end
Method: generate the covariance matrix
- Compute the J covariance integral from residue calculus.
- Build the covariance matrix in block form. Note parts of it have Toeplitz structure.
- Find the Cholesky decomposition. If due to numerical errors the eigenvalues are not positive, decompose the matrix diagonally, replace negative EV by small positive value, rebuild the matrix.
- Commented out: rebuild the matrix
function GenerateCovMat(obj) numTsteps = obj.parameters.numTsteps; time = obj.parameters.time; cGLE = obj.parameters.cGLE; tVec = obj.resCalc.tVec; numK = obj.parameters.numKernels; aGLE = obj.parameters.aGLE; gamma = obj.parameters.gamma; resVec = obj.resCalc.resVec; omegaVec = obj.resCalc.omegaVec; JInt = NaN(length(time),1); for jindex=1:length(time) JInt(jindex) = cGLE^2*(time(jindex)*tVec(numK+1)/... (aGLE*tVec(numK+1)+1i*gamma*tVec(numK))... +sum(imag(resVec./omegaVec.^2 ... .*(exp(1i*time(jindex)*omegaVec)-1)))); end numBlocks = min(2^10,numTsteps); count = numTsteps/numBlocks; % Build the covariance matrix in block form matA = zeros(numBlocks,numBlocks,count,count); jVal = zeros(numBlocks+1,count); for iindex=1:count jVal(:,iindex) = JInt(1+(iindex-1)*numBlocks:1+iindex*numBlocks); end for iindex=1:count for jindex=1:iindex matR3 = repmat(jVal(2:end,jindex)',numBlocks,1); matR1 = repmat(jVal(2:end,iindex),1,numBlocks); if iindex==jindex matR2 = toeplitz(jVal(1:end-1,1)); else matR2 = toeplitz(jVal(1:end-1,iindex-jindex+1),... flipud(jVal(2:end,iindex-jindex))'); end matA(:,:,iindex,jindex) = matR1-matR2+matR3; end end % Find the Cholesky matL = zeros(numBlocks,numBlocks,count,count); tol = 1e-8; for iindex=1:count for jindex=1:iindex if iindex==jindex temp = 0; for kindex=1:iindex-1 temp = temp+squeeze(matL(:,:,iindex,kindex))... *squeeze(matL(:,:,iindex,kindex))'; end try matL(:,:,iindex,jindex) = chol(squeeze(... matA(:,:,iindex,jindex))-temp,'lower'); catch [matV,matD]=eig(squeeze(matA(:,:,iindex,jindex))... -temp,'nobalance'); vecD = diag(matD); fprintf('ERROR: Matrix is not positive definite.\n') fprintf('Largest negative EV %6.4e .\n',min(vecD)) vecD(vecD<0)=tol; matC = matV*diag(vecD)/matV; matL(:,:,iindex,jindex) = chol(matC,'lower'); end else temp = 0; for kindex=1:jindex-1 temp = temp+squeeze(matL(:,:,iindex,kindex))... *squeeze(matL(:,:,jindex,kindex))'; end matL(:,:,iindex,jindex) = (squeeze(matA(:,:,iindex,jindex))... -temp)/(squeeze(matL(:,:,jindex,jindex))'); end end end %{ % Rebuild the matrix matC = zeros(numTsteps,numTsteps); for iindex=1:count for jindex=1:iindex matC(1+(iindex-1)*numBlocks:iindex*numBlocks,... 1+(jindex-1)*numBlocks:jindex*numBlocks) = ... matL(:,:,iindex,jindex); end end obj.dataCovMatC = matC; %} obj.dataCovMatL = matL; end
Method: generate paths
Generate the paths in block form. Simply multiply the covariance matrix by a normal Gaussian vector.
function GeneratePaths(obj) numPaths = obj.parameters.numPaths; numTsteps = obj.parameters.numTsteps; numBlocks = min(2^10,numTsteps); count = numTsteps/numBlocks; matL = obj.dataCovMatL; pathTemp = zeros(numBlocks,numPaths,count); matY = zeros(numBlocks,numPaths,count); for iindex=1:count matY(:,:,iindex) = randn(numBlocks,numPaths); end for iindex=1:count for jindex = 1:iindex pathTemp(:,:,iindex,jindex) = matL(:,:,iindex,jindex)... *matY(:,:,jindex); end end pathBlock = sum(pathTemp,4); for iindex = 1:count obj.dataPath(1+(iindex-1)*numBlocks:iindex*numBlocks,:) = ... pathBlock(:,:,iindex); end end
Method: find MSD
function FindMSD(obj) obj.dataMSD = squeeze(mean(obj.dataPath.^2,2)); end
Method: find increment ACF
Uses acf function on each path.
function FindIncACF(obj,numTACF) numPaths = obj.parameters.numPaths; xACF = zeros(numTACF-1,numPaths); for jindex=1:numPaths xACF(:,jindex) = acf(diff(obj.dataPath(:,jindex)),0:numTACF-2); end obj.dataIncACF = squeeze(mean(xACF,2)); end
Method: find MFPT
Input: layer width and sim object (paths)
- Calculate the exit time and the number of survivors. If a path hasn't exited, it is given the value of the maximum time.
- Deal with survivors: only if the relative number of survivors is bigger than
 . This guantees less than kappa paths survives. Increase the time step by a factor
. This guantees less than kappa paths survives. Increase the time step by a factor 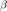 . Regenerate covariance matrix and paths. Compute exit time and survivors. Repeat until condition is met.
. Regenerate covariance matrix and paths. Compute exit time and survivors. Repeat until condition is met. - Calculate the first passage time when the maximum time is long enough to guarantee enough survivors. Adjust for the exit time by fitting the tail of the distribution by an exponential.
- Calculate mean and standard deviation.
function FindMFPT(obj,width) numPaths = obj.parameters.numPaths; numTsteps = obj.parameters.numTsteps; kappa = obj.parameters.kappa; beta = obj.parameters.beta; tFinal = max(obj.parameters.time); time = obj.parameters.time; FPT = zeros(length(width),numPaths); meanFPT = zeros(length(width),1); stdFPT = zeros(length(width),1); survivors = zeros(length(width),numTsteps+1); for iindex=1:length(width) fprintf('Working on width %d microns\n',width(iindex)) % Caclulate the exit time and number of survivors at the end exitInd = zeros(numPaths,1); numSurvivors = zeros(numTsteps+1,1); for jindex=1:numPaths temp = find((abs(obj.dataPath(:,jindex))>width(iindex))... ,1,'first'); if isempty(temp) exitInd(jindex) = numTsteps; else exitInd(jindex) = temp; end end exitTime = exitInd*obj.parameters.dt; numSurvivorsFinal = sum(exitTime >= tFinal); % Deal with the survivors if numSurvivorsFinal>0 while (numSurvivorsFinal/numPaths > kappa) obj.parameters.dt = beta*obj.parameters.dt; fprintf(['Not enough survivors, increasing the ' ... ' time step to %d.\n'],obj.parameters.dt) obj.parameters.time = (0:obj.parameters.numTsteps)... *obj.parameters.dt; tFinal = max(obj.parameters.time); time = obj.parameters.time; obj.GenerateCovMat; obj.GeneratePaths; for jindex=1:numPaths temp = find((abs(obj.dataPath(:,jindex))>... width(iindex)),1,'first'); if isempty(temp) exitInd(jindex) = numTsteps; else exitInd(jindex) = temp; end end exitTime = exitInd*obj.parameters.dt; numSurvivorsFinal = sum(exitTime >= tFinal); end end for jindex = 1:numTsteps+1 numSurvivors(jindex) = sum(exitTime>=time(jindex)); end % Calculate first passage time and adjust for the survivors relnumSurvivors = numSurvivors/numPaths; if numSurvivorsFinal>0 expFit = fit(time',relnumSurvivors,'exp1'); exitTime(exitInd==numTsteps) = ... exitTime(exitInd==numTsteps)-1/expFit.b; end survivors(iindex,:) = relnumSurvivors; FPT(iindex,:) = exitTime'; meanFPT(iindex) = mean(exitTime); stdFPT(iindex) = std(exitTime); end obj.dataSurvivors = survivors; obj.dataFPT = FPT; obj.dataMFPT = meanFPT; obj.dataSMFPT = stdFPT; end
The end
end
end